Expected heterozygosity
\[H_{e} = 1 - \sum{p_{i}^{2}} \]
Unbiased \(He\)
- True value from population allele frequencies
- Estimate based on sample
- Small samples miss rare alleles
\[\hat{He} = \left(\frac{n}{n-1}\right) \left(1 - \sum{p_{i}^{2}}\right)\]
Segregating sites
\[S = 3\]
\[p_s = \frac{S}{L} = \frac{3}{14} = 0.21\]
Nucleotide diversity
Average number of differences between pairs of sequences
\[\pi = \sum_{j=1}^{S} He_j\]
\[E\left(\pi\right) = \theta = 4N\mu\]
\[He_3 = \left(\frac{4}{3}\right) \left(1 - (0.5^2 + 0.5^2)\right) = 0.\dot{6}\]
\[He_8 = \left(\frac{4}{3}\right) \left(1 - (0.75^2 + 0.25^2)\right) = 0.5\]
\[He_{11} = \left(\frac{4}{3}\right) \left(1 - (0.75^2 + 0.25^2)\right) = 0.5\]
\[\pi = 0.\dot{6} + 0.5 + 0.5 = 1.\dot{6}\]
Estimating theta
Because
\[E\left(\pi\right) = \theta = 4N\mu\]
\[\hat{\theta_\pi} = \pi = \sum_{j=1}^{S} He_j\]
Watterson’s theta
\[\hat{\theta_W} = \frac{S}{a}\]
\[a = \sum_{i=1}^{n-1} \frac{1}{i}\]
\(S = 3\), \(n = 4\)
\[\hat{\theta_W} = \frac{3}{\frac{1}{1} + \frac{1}{2} + \frac{1}{3}} = 1.\dot{6}\dot{3}\]
Site frequency spectrum
Infinite sites model: all sites biallelic
![]( "Site frequency spectrum plot")
Which allele?
![]( "Simple primate evolutionary tree")
Derived alleles
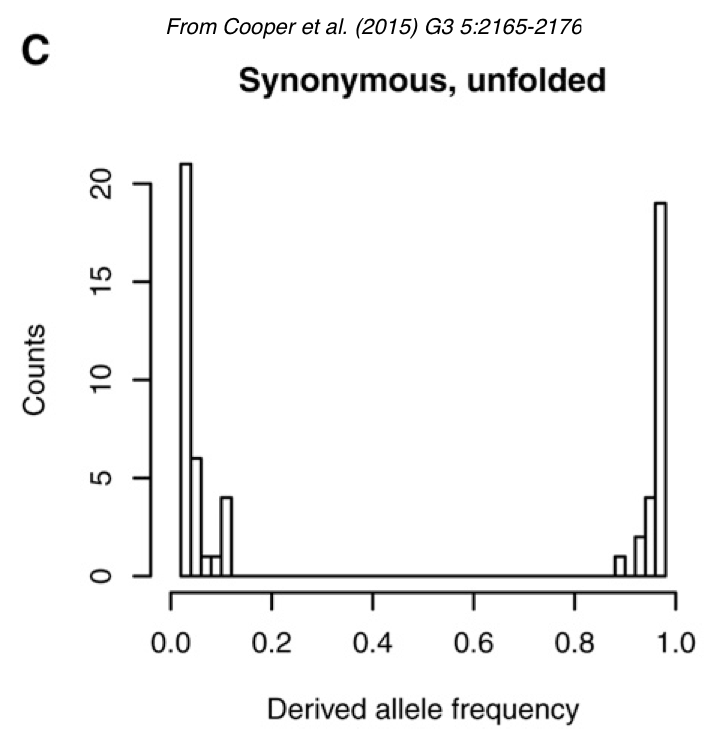
“Unfolded” spectrum
- Drosophila melanogaster mitochondrial DNA
- Derived alleles
- Outgroup: D. yakuba
- Most sites, 1 rare allele
Folded SFS
- Ancestral / derived status unknown
- Use “minor allele frequency” (MAF)
- Frequency < 0.5
![]( "Site frequency spectrum for fall armyworm")
Reading
No assigned reading.
